[논문정리] Cnvlutin: Ineffectual-Neuron-Free Deep Neural Network Computing

Cnvlutin: Ineffectual-Neuron-Free Deep Neural Network Computing

Abstract

현재의 DNNs(Deep Neural Networks)는 0 곱셈도 진행해서 비효율적임.

→ Cnvlutin(CNV) : 정확성 손실 없이 이런 비효율적인 과정 모두 제거

- hierarchical data-parallel unit(계층적 데이터 병렬 유닛) 사용
- group들이 독립적으로 진행되는 걸 가능하게 함 → 비효율적인 계산 건너뜀
- co-designed data storage format이 병렬 유닛에서 조절을 할 수는 있지만 경로에서 계산을 하지 않도록 함

 

units + data storage → 데이터 병렬 구조를 만들어 메모리 계층 구조에서 정렬된 접근을 가능하게 하면서 데이터를 많이 전송(data lanes busy)

Introduction

DNN 중 특히 CNN은 물체 인식 알고리즘, 이미지 분류에서 특히 뛰어나다

DNN은 새로운 것이 아니지만 계산 공간을 많이 쓸 수 있어지면서 전성기를 맞음

앞으로도 DNN은 연산량도 많아지고 input도 커지고 할 것 → real time에서는?

에너지 사용을 줄인 작은 하드웨어도 필요!

연산에 쓰이는 content를 고려하여 진행하자

DaDianNao 가속기를 발전시켜 CNV를 개발

DaDianNao는 SIMD를 사용하였지만 input이 0인 경우 넘어갈 수가 없었다

CNV 유닛은 lane들을 작게 나누어 필요없는 연산을 수행하지 않도록 한다

Motivation

여러개의 삼차원 필터와 input

input이나 뉴런들과 필터 weight,시냅스의 내적 연산들의 합이 하나의 output이 된다

가장 중요한 motivation이 많은 뉴런이 0이 된다는 것

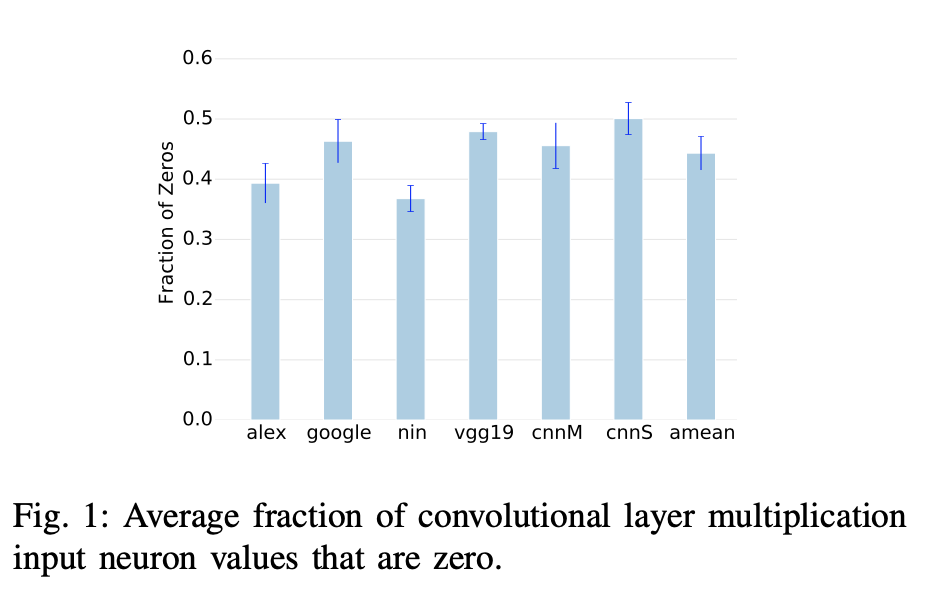
왜 이렇게 많은 0 값이 있을까?

DNN의 특성 때문

DNN은 특정 학습된 feature가 존재하는지, 존재한다면 어디에 있는지 등을 알아내려고함

feature가 존재한다면 뉴런에 양의 값이 output으로, 없다면 0

대부분 0이 들어가는게 당연하고 모든 feature가 존재하지 않을 수도 있다

이런 특성으로 Recifier,ReLU 레이어처럼 음수는 0으로 바꾸는 레이어도 있다

이렇게 많은 0의 값을 가진 뉴런이 만들어지지만 그 위치는 Input값에 의해 결정된다

→ 항상 0의 값을 갖는 뉴런은 없거나 있어도 매우 적다

convolutional layer를 계산하는데 드는 시간은 element의 수에 선형비례

→ zero value 뉴런을 skip해서 upper bound보다 작은 실행 시간을 만들자

Enabling Zero Skipping : A Simplified Example

두가지 핵심 아이디어

1. lane decoupling
2. storing the input on-the-fly in an appropriate format that facilitates the elimination of zero valued inputs

A. input이 0일때 처리 과정 설명

B. DNN에서 사용 가능한 여러 그룹의 processing lane을 묶어 큰 SIMD 유닛으로 만든 accelerator 구조를 설명

C. processing lane을 나누어 각자 처리할 수 있도록 하는 구조에 대해 설명 → zero skipping이 가능하도록

추가로 lane group이 연산을 각자 시작할때 문제도 존재

 

 

A. Computation of Convolutional Layers

CNN의 연산은 DNN과 비슷하지만 가장 큰 차이는 input에서 특정 feature를 찾기 위해 weight을 반복해서 사용한다는 점이다

input

삼차원 실수 배열

$I_x * I_y * i$

첫번째 layer에서 input으로 쓰이고 다음 layer에 output 뉴런 전달

filter

$F_x * F_y * i$

각 레이어는 N개의 필터를 x,y 축을 따라 적용

output

$O_xO_yN$

계산을 위해 필터가 input neuron(window)에 적용된다

한개의 window와 filter의 곱으로 한개의 output neuron이 생긴다

필터는 Input에서 stride S만큼 이동하면서 전체 output을 생성

3 X 3 X 2 input neuron

한개의 2 X 2 X 2 filter

2 X 2 X 1의 output neuron을 생성

→ 이 때 input neuron이 0이라면 이 과정은 하지 않아도 되는 과정이고 여기서 결과값에 상관 없이 시간과 에너지 절약 가능

만약 2 X 2 X 2의 filter가 두개라면 (b),(c)를 통해 알 수 있듯이 output이 2 X 2 X 2가 된다

 

 

B. The Simplified Baseline Architecture

기본 아키텍쳐는 DaDianNao state- of-the-art accelerator를 기반으로 함

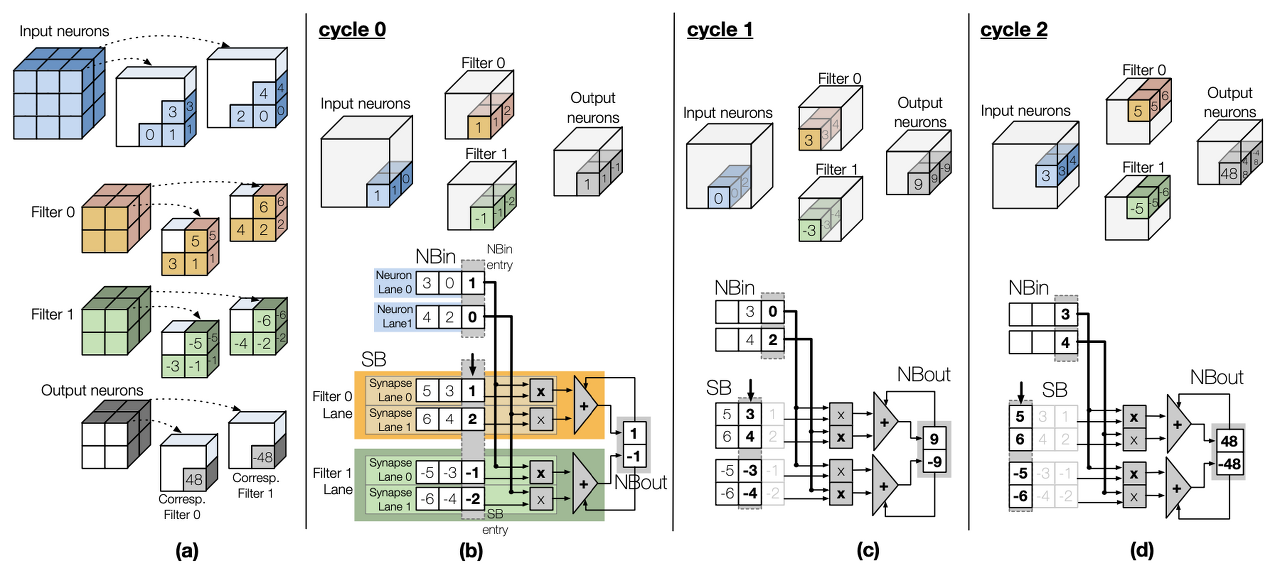
a) input : 322 → 필터 거치면서 (222짜리 두 개 ) → output : 222

b) neuron lane 2개, filter lane 2개(filter lane은 synapse lane을 두개씩 각자 갖고 있다)

각 neuron lane,과 synapse sublane은 input neuron buffer(NBin), Synapse Buffer(SB)에서 값을 받는다

매 사이클마다 각 neuron lane은 synapse sublane에게 값을 전달한다

각 synapse syblane은 뉴런과 시냅스의 input으로 들어온 값을 곱하고 필터 lane별 adder tree가 부분합 생성 후 output neuron buffer(NBout)에 그 값을 더한다

이런 layer 연산 구조의 장점은 유닛이 모든 뉴런과 필터 lane을 결합시켜 lock-step을 진행 가능하다는 점이다

→ 모든 연산 수행시 좋은 성능 but zero skip 불가능

 

C. The Simplified Cnvlutin Architecture

모든 Neruon lane이 결합되지 않고 독립적으로 진행할 수 있도록 CNV 사용

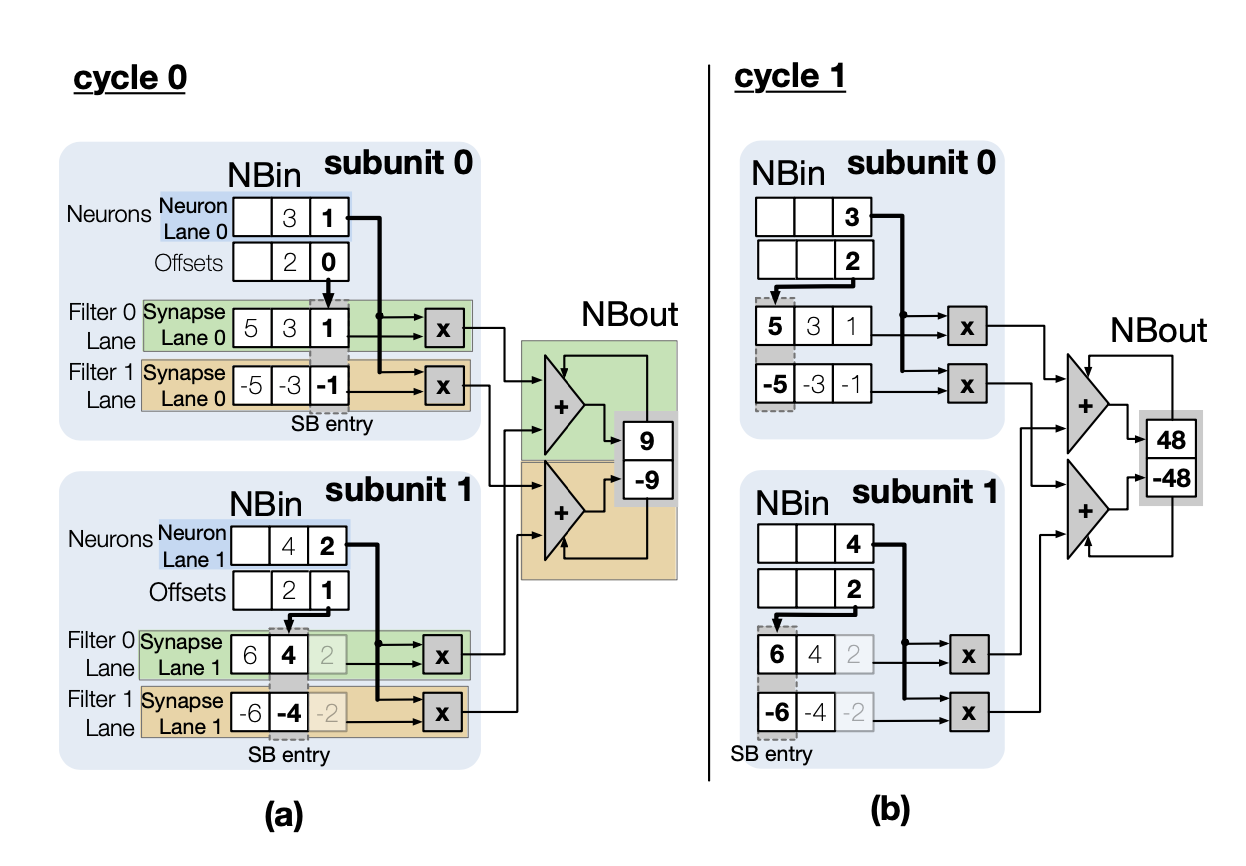
1) back-end : adder tree + NBout

2) front-end : neuron lanes, synapse sublanes, multipliers

두 파트로 구분

벡엔드는 변화 X

프론트엔드가 한개의 neuron lane당 두개의 subunit으로 분리

각 subunit은 한개의 neuron lane과 synapse sublane으로 구성 ( 각 필터에 대해 )

매 사이클마다 각 subunit은 두개(필터별로)의 곱을 생성한다

 

두개의 adder tree는 이 곱을 받아 부분 output neuron sum을 계산

→ zero skip 가능한 구조

 

input에 0이 있을 때 neuron lane이 skip 하는게 아니라 하드웨어가 zero neuron을 제거하는 것이 목표

→ 0이 아닌 값만이 NBin으로 전달

 

Input neuron은 Zero-Free Neuron Array format(ZFNAf)로 저장

neuron lane 중 0이 아닌 lane만 진행 하기 위해 0인 뉴런이 제거되면 맞는 SB를 찾아야 한다

따라서 ZFNAf 형식은 offset 사용

ex) neuron의 스트림 (1,0,0,3) → ((1,0),(3,3))

offset을 이용해서 SB sublane의 index 설정 가능

The CNVlutin Accelerator

A. Baseline Architecture

DaDianNao 칩 기반

DaDianNao 칩은 16개의 Neural Functional Units(NFU) 포함

(a)가 한개의 NFU를 나타내는 그림

매 사이클마다 유닛들은 16개의 input neuron, 16개의 필터로부터의 256개의 synapse를 처리

→ 16개의 neuron lane, 16개의 filter lane, 한개의 filter lane은 16개의 synapse lane

→ 16개의 부분합을 16개의 output neuron으로

→ 256개의 곱셈기, 16개의 17-input adder tree(16개의 곱셈, 1개의 기존 부분합이라 17)

 

각 neuron lane은 16개의 16개의 필터로부터의 synapse lane과 각자 연결되어있고 lock-step

이러한 NFU를 사용하는 DaDianNao는 off-chip bandwidth를 최소화하고 on-chip compute utilization을 최대화하고자 하는 용도

total SB capacity는 처리중인 모든 synapses를 저장하기 충분하도록 설계됨 →off-chip에서 synapses를 fetching하는 것을 방지

최대 256개의 필터 병렬 처리 가능 (유닛 당 16개)

initial input과 final output을 제외한 모든 inter-layer neuron output들은 eDRAM이나 Neuron Memory(NM)에 저장됨

NM은 16개의 unit에 공유됨. 4MB로 디자인되어있다

 

외부에서 보이는 트래픽은 초기입력, layer당 한 번 synapses loading하기, final output 적기밖에 없음

Processing: 외부 메모리를 읽는 것으로 시작 ( 외부메모리 : 1. filter synapses, 2. initial input )

filter synapses : SB에 분배됨

initial input(neuron input) : NBins에 들어감

 

layer output은 NBout을 통해 NM에 저장됐다가 다음 layer processing을 위해 NBins로 들어감

필요할 경우 외부 메모리에서 다음 synapses를 읽어오는 게 현재 layer 처리와 중복될 수 있음

NM이나 SB 단일 노드로 처리할 수 있는 크기보다 큰 DNN 처리를 위해서 multiple nodes 사용 가능

eDRAM을 사용하여 NM과 SB를 향상시킬 경우, 용량이 클수록 싱글 칩으로 더 많은 neuron과 filter process 가능 ( 외부 메모리 spiling, 과도한 off-chip 접근 없이 )

 

1) Processing Order in DaDianNao

a) DaDianNao architecture가 256개 filter를 동시에 적용하는 input neuron array process하는 방법

각 unit은 16개의 필터를 처리함(0~15, 16~31, ... , 240~255)

그림은 간단하게 i차수에 대한 요소의 위치만 표기해놨음

ex) filter 7의 위치(0,0,15) → $s^7_{15}$ )

 

16개의 input neuron의 fetch block이 매 사이클마다 16개의 unit에 fetch...?

fetch block은 synapse lane 한개마다 neuron 한개, unit 한개마다 16개의 filter lane

ex)

0번째 사이클

fetch block에는 뉴런(0,0,0)~(0,0,15)

n(0,0,0)은 unit 0에서 $s^0(0,0,0)$

$s^{15}(0,0,0)$에, unit15에서 $s^{240}(0,0,0)$

 

$s^{255}(0,0,0)$에 곱해진다

다음에는 n(0,0,1)이 전부 곱해지고 ... 반복

이 때 synapse는 SB에 그림과 같이 저장

 

해당 window의 연산이 종료되면 좌표만 바꾸면 되니까 다음 window에서 연산 시작이 쉽다

여기서는 zero skip 없이 모든 것 다 연산

 

B. Cnvlutin Architecture

front-end : neuron lane과 synapse lane으로 이루어져있다, 각각은 한개의 neuron lane과 16개의 synapse lane이 들어있다, synapse lane은 총 16개로 각각 한개의 필터를 의미 매 사이클마다 각 subunit은 neuron,offset 한 pair를 NBin에서 가져온다, offset은 SBin으로 잘 연결하기 위해 사용, 필터별로 한개 즉 총 16개의 Product가 생성된다

 

back-end : 그대로, 16 X 16 곱을 16개의 subunit으로부터 받는다, 16 adder tree 사용, adder tree는 16개의 부분 output neuron 값을 축적해서 64 NBout에 넣는다 subunit NBin은 64 entry, 각 entry는 16비트 fixed-point value, offset field를 갖고있다

SB capacity는 유닛당 2MB(DaDianNao와 같게), 각 subunit은 128KB (128 * 16 = 2MB)

각 subunit은 16synapse의 16*16 bit를 갖고 있다

128KB = $2^{17}$byte

16 * 16 bit = 32 byte = $2^5$ byte

2^5 * ... 계산 헷갈림ㅠㅠ

 

결론 : 모든 subunit은 16개의 neuron lane, 256개의 synapse lane → 16개의 부분 output neuron을 각 filter에 맞게 생성

CNV unit은 encoded, conventional neuron array 생성

유닛이 offset field를 사용할 지 안할지 알려주는 configuration flag를 사용

challenges

1. 실시간으로 encoded neuron array 만들기
2. 모든 unit과 lane을 계속 사용(busy)
3. 중앙 eDRAM에 접근하는 순서를 그대로 유지

→ input neuron array를 encode 하기 위해 unit으로 분할된 방식 사용

1) The Zero-Free Neuron Array Format(ZFNAf)

0인 값들을 계산하지 않을 수 있도록 하는 형식

non zero neuron만 offset과 함께 저장

→ 어떤 neuron이 critical path에서 연산될지 정해준다

 

CSR format과 비슷하지만 차이점 존재

CSR은 0이 아닌 값만 저장하면서 memory footprint도 줄이는 것이 목적

ZFNAf는 0이 아닌 값만 저장하는 것이 목적

→ all lane을 busy하게 사용하기 위해 memory footprint 희생

 

neuron을 value, offset pair로 encode → bricks

brick들은 정렬되어 있고 연속적

모두 x,y 좌표가 같다

convolutional 3d array format에 first neuron이 저장되었어야 할 위치에 brick이 대신 저장

두개의 속성

1. 뉴런의 첫번째 brick의 좌표만 가지고도 indexing 할 수 있어야 한다
2. offset을 저장하는 overhead를 줄이기 위해 offset field를 작게 유지해야한다
   CNV unit이 16개의 lane만 사용하므로 offset field는 4bit면 충분
   25% capacity overhead

2) Processing Order in CNV

DadianNao : 사이클마다 16개 neuron의 fetch block을 fetch하여 16 unit에 전달 → 256개의 필터에 적용

CNV : ZFNAf의 block은 하나의 brick을 가지고 0이 없을때만 적용

모든 lane을 busy하게 유지하기 위해서 각 lane별로 다르게 행동

input window를 16개로 slice, 모든 slice는 세로로 잘려서 z 좌표가 같다

매 사이클마다 slice 한개가 neuron 하나와 fetch되어 모든 lane을 busy하게 유지

 

ex

e(x,y,x) → ZFNAf의 좌표 (x,y,z)가 갖는 (neuron, offset)

cycle 0

e(0,0,0), e(0,0,16) ... e(0,0,240)이 fetch

cycle 1

만약 두번째 뉴런도 모두 0이 아니라면

e(0,0,1), e(0,0,17) ... e(0,0,241)이 fetch

 

0인 경우는 pass

만약 e(0,0,0)외의 brick0의 모든 뉴런이 0이라면 e(1,0,0)으로 넘어간다

 

그 block이 얼마나 많은 0의 값을 갖는가에 따라 각 neuron lane이 독립적으로 시행

 

ex

만약 e(0,0,0)이 j라면

cycle 0일때 unit 0의 subunit 0은 $s^0$ (0,0,j)

 

$s^{15}$(0,0,j)가 필요하고 subunit15는 $s^0$ (0,0,240+j)

$s^{15}$(0,0,240+j), unit15의 subunit 0은 $s^{240}$ (0,0,j)~$s^{255}$(0,0,j)

 

3) The Dispatcher

dispatcher는 entry 당 한개의 brick을 담을 수 있는 16-entry Brick Buffer(BB)를 갖는다

각 BB entry는 한개의 NM bank랑 연결되어 neuron lane에 값을 전달

ex

BB[0]은 NM bank 0에서 neuron brick을 가져와 모든 유닛의 neuron lane 0에 전달

 

dispatcher는 모든 bank의 brick을 읽어 총 16개의 brick을 읽는 것으로 시작

그리고 non-zero neuron을 neuron lane에 각각 보낸다

 

4) Generating the ZFNAf

DNN에 처음 들어오는 input은 conventional 3D array format의 이미지

첫번째 레이어는 3-feature deep neuron array로 input을 다루어 각 color plane을 feature라고 생각

나머지 convolutional layer는 CNV가 만든 ZFNAf를 사용

encoder가 input을 ZFNAf 포맷으로 만든다

encoder는 16개의 input buffer와 16개의 encoded-neuron output buffer, offset counter를 사용

매 사이클마다 인코더는 다음 뉴런을 IB에서 읽고 offset counter를 증가시킨다

값이 0이 아니라면 뉴런은 offset counter 값과 함께 OB에 복사된다

모든 IB를 읽으면 OB는 ZFNMf를 NM으로 보낸다

 

5) Synchronizaiton

모든 unit은 같은 window에서 뉴런 처리, 다음 window는 지금 window가 process된 후에만 진행됨

CNV는 백엔드랑 control의 수정을 막기 위해 이 방식을 따름

모든 lane이 같은 수의 0을 갖지 않으면, 뉴런 lane은 각자 독립적으로 brick을 처리 → 다른 lane보다 빨리 끝나는 lane 있을 수 있음 → 다른 lane이 끝날 때까지 기다림.